Boomdiagram

Soms moet je rekening houden met bepaalde factoren als je een boomdiagram maakt. Hieronder staat een boomdiagram van de wedstrijd SOD tegen MNM die in 3-2 eindigde. Het scoreverloop van de wedstrijd heeft op 10 verschillende manieren kunnen verlopen (som 25 - hoofdstuk 7 - havo - editie 8)::

Stelling van Pythagoras

Kansen en tellen

Hieronder staat uitgelegd hoe een boomdiagram werkt:

Nog meer uitleg, voorbeelden en oefeningen over een wegendiagram, een rooster en een venndiagram kun je vinden op math4all

bordaantekening klas 1 hoofdstuk 8 pijlenketting

Gemiddelde, modus, mediaan op de GR

Frequentiepolygoon, staafdiagram en boxplot op de GR

Frequentiepolygoon

Frequentie-polygoon

Als je bij een histogram de middens van elk staafje verbindt met rechte lijntjes krijg je een zogenaamd frequentie-polygoon.

Voorbeeld:


De staafjes teken je uiteraard niet. Je krijgt dan de volgende grafische voorstelling:



Uiteraard zet je bij de assen natuurlijk wel waar het over gaat. In plaats van de frequentie kun je ook de relatieve frequentie gebruiken.

Bron:: wiswijzer

Oppervlakte cilinder

Een cilinder bestaat uit 3 delen:: de bodem, de deksel en de zijkant (dit noemen ze de mantel). Van deze delen gaan we apart de oppervlakte berekenen::

De bodem is een cirkel, de oppervlakte van een cirkel is straal x straal x pie. De straal is de helft van de diameter (doorsnede) en we noemen de straal in de wiskunde ook wel R (van Radius). 

De deksel is precies even groot als de bodem, het antwoord van de bodem is dus hetzelfde als die van de deksel! LET OP:: soms moet je de oppervlakte berekenen van een cilinder zonder deksel (denk aan een prullenbak).

Het tussenstuk wordt een rechthoek als je deze zou openvouwen. Kijk maar naar de tekening hier onder::

De oppervlakte van een rechthoek is lengte x breedte. De lengte is hetzelfde als de hoogte van de cilinder, de breedte is hetzelfde als de omtrek van de bodem van de cilinder. Lengte x breedte wordt dan:: diameter x pie x hoogte.

De drie delen tel je daarna bij elkaar op en je hebt de oppervlakte van de cilinder berekend!

Bordaantekeningen hoofdstuk 8 (Havo 3 - ABCFormule)

Bordaantekeningen Hoofdstuk 6 (Havo 3 - Sin/Cos/Tan)

Alle uitslagen van een kubus

Hieronder is een kubus getekend.

kubus

Als steeds een ribbe wordt doorgeknipt, dan zijn op een bepaald moment
de zijvlakken in een plat vlak neer te leggen, terwijl ze nog wel aan elkaar vast zitten.
Zo'n doorgeknipte en uitgevouwen vorm heet een "uitslag". Een uitslag is eigenlijk een bouwplaat zonder plakranden!

Hieronder zie je die uitslag.

uitslag

Kubus tekenen

Aanzichten

Boven-, voor- en zijaanzicht

 

We leven in een ruimtelijke wereld. Bijna niets is plat. Maar als je een ruimtelijk figuur tekent of op de foto zet, kan het lijken dat het wel zo is. Om de ruimtelijk dan weer te kunnen zien, heb je verschillende aanzichten nodig.
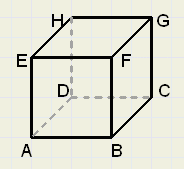
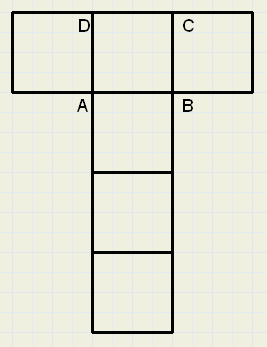
Om een goed beeld van een ruimtelijke figuur te krijgen, kijk je er van verschillende kanten naar. Je stelt je daarbij voor dat de hele figuur in een doorzichtige balk past. Op de voorkant van de balk teken je wat je van die kant ziet: het vooraanzicht. Op de bovenkant komt het bovenaanzicht. Op de zijkant komt het zijaanzicht.

Als je deze drie aanzichten zo in één figuur zet, dat je die balk weer kunt vouwen, spreek je van een drieaanzicht van de figuur.

Kubussen

Hier zie je drie aanzichten van een stapel kubussen. Om volledig te zijn zie je in het bovenaanzicht hoeveel kubussen er op elkaar liggen. Eigenlijk zijn dan het vooraanzicht en het zijaanzicht overbodig geworden. Maar als je niet in één van de aanzichten aangeeft hoeveel kubussen er boven elkaar of achter elkaar of naast elkaar liggen, heb je aan de aanzichten alleen niet genoeg om de kubusstapel te bouwen. Er zijn dan meerdere mogelijkheden.

Architectuur

 

Ook architecten werken met aanzichten. Hiernaast zie je een voorbeeld van verschillende aanzichten van een huis.

Meten in aanzichten

Als je van het vogelhokje bovenaan de pagina de afmetingen van het dak wilt bepalen moet je in het juiste aanzicht meten. Kijk maar naar het plaatje.

Puzzel

 

Hier zie je een vooraanzicht en een zijaanzicht van een stapel kubussen.
Het bovenaanzicht ontbreekt. Hoeveel kubussen heb je hier minstens voor nodig? En hoeveel passen er hoogstens in? Als antwoord kun je het beste een bovenaanzicht tekenen met het aantal op elkaar gestapelde kubussen er in.

Bron: Math4all

Een toets voorbereiden

Je kunt op veel verschillende manieren een toets (voor wiskunde) voorbereiden. Er bestaat niet 1 manier die goed is, maar wel 100 (of meer)..... Sommige dingen werken wel beter dan anderen. Hieronder staat hoe ik denk dat je het beste kunt voorbereiden::

• Neem het hele hoofdstuk door en schrijf alle woorden/zinnen op die belangrijk zijn en maak zo een samenvatting van het hoofdstuk. Alle woorden die je hebt opgeschreven moet je tijdens je toets kennen en kunnen toepassen. Voorbeeld. 
• Test je kennis door de Extra Oefeningen te maken (basiskennis). De + oefeningen zijn belangrijk voor de onderbouw (Havostof). De Gemengde oefeningen zijn belangrijk voor de bovenbouw (lijkt een beetje op examensommen)
• Als je ergens niet uitkomt ga je bladeren in je boek (b.v. naar je samenvatting of naar de paragrafen in het hoofdstuk) of kijk je naar de aantekeningen die je hebt gemaakt. De bedoeling is dat je erachter komt welke strategie je nodig hebt om het probleem op te lossen.
• De sommen die je geoefend hebt kijk je heel precies na: als een antwoord net niet goed is dan is het fout. Kijk ook of je de berekeningen en eenheden goed hebt opgeschreven.
• Besteed niet in 1 keer heel veel tijd aan het voorbereiden, maar doe elke dag een beetje. Het is goed om het gemaakte werk de volgende dag nog een keer te maken, zodat je sommen herkent.

Waarop je tijdens de toets moet letten lees je HIER!

Voorbereidingen toets H9 - vergelijkingen (klas 2)

Als ik het hoofdstuk doorblader vallen de volgende woorden/stukjes zin me op::

• Formules korter schrijven
• gelijksoortige termen
• h is hetzelfde als 1h
• vergelijking
• omgekeerde pijlenketting
• oplossing
• balans
• evenwicht
• weghalen
• links en rechts hetzelfde
• beide kanten van de = letters
• omslagpunt
• snijpunt van 2 lineaire (rechte) grafieken
• vergelijking maken en die oplossen
• + Ongelijkheden
• < of > (kleiner of groter)
1. maak een vergelijking
2. los deze op
3. getallen groter of kleiner dan de oplossing invullen en geef op getallen lijn of ze voldoen of niet
4. schrijf de oplossing op
• formule
• maak een formule
• maak een tabel
• maak een grafiek

Als je al deze woorden kent, maar ook kunt gebruiken, dan ben je klaar voor je toets! Je kunt jezelf testen door de Extra oefening te maken voor de basisstof (Mavo) en de + opdrachten voor de Havostof. Lukt iets niet, dan kun je in de samenvatting of in je schrift kijken welke strategie je moet gebruiken om het probleem op te lossen. Het is heel belangrijk dat je je werk heel precies nakijkt: in de wiskunde is een antwoord niet ongeveer goed, maar precies!